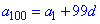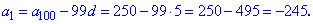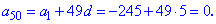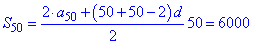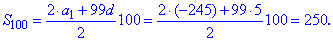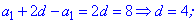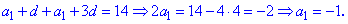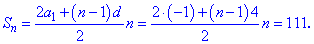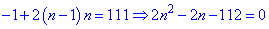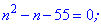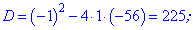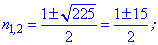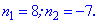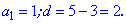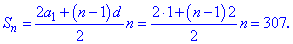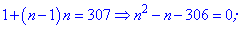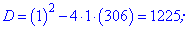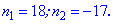|
||||||||
Арифметична прогресія. Формули та приклади
Арифметична прогресія. Формули та приклади
в якій кожен наступний член відрізняється від попереднього на сталий доданок, який ще називають кроком або різницею прогресії.
Таким чином, задаючи крок прогресії та її перший член можна знайти будь-який її елемент за формулою
Властивості арифметичної прогресії1) Кожен член арифметичної прогресії, починаючи з другого номера є середнім арифметичним від попереднього та наступного члена прогресії
Обернене твердження також вірне. Якщо середнє арифметичне сусідніх непарних (парних) членів прогресії рівне члену, який стоїть між ними то дана послідовність чисел є арифметичною прогресією. За цим твердженням дуже просто перевірити будь-яку послідовність. Також за властивістю арифметичної прогресії, наведену вище формулу можна узагальнити до наступної
В цьому легко переконатися, якщо розписати доданки справа від знака рівності
Її часто застосовують на практиці для спрощення обчислень в задачах. 2) Суму n перших членів арифметичної прогресії обчислюють за формулою
Запам'ятайте добре формулу суми арифметичної прогресії, вона незамінна при обчисленнях та досить часто зустрічається в простих життєвих ситуаціях. 3) Якщо потрібно знайти не всю суму, а частину послідовності починаючи з k-го її члена, то в нагоді Вам стане наступна формула суми
4) Практичний інтерес має відшукання суми n членів арифметичної прогресії починаючи з k-го номера. Для використовуйте формулу
На цьому теоретичний матеріал добігає кінця і переходимо до розв'язування поширених на практиці задач. ЧИТАЙТЕ ТАКОЖ: Куб числаПриклад 1. Знайти сороковий член арифметичної прогресії 4;7;... Розв'язання: Згідно умови маємо
Визначимо крок прогресії
За відомою формулою знаходимо
ЧИТАЙТЕ ТАКОЖ: ЛОГАРИФМ числа Приклад 2. Арифметична прогресія задана третім та сьомим її членом Розв'язання: Розпишемо задані елементи прогресії за формулами
Від другого рівняння віднімемо перше, в результаті знайдемо крок прогресії
Знайдене значення підставляємо в любе із рівнянь для відшукання першого члена арифметичної прогресії
Обчислюємо суму перших десяти членів прогресії
Всі шукані величини знайдені. ЧИТАЙТЕ ТАКОЖ: Відсоток від числа Приклад 3. Арифметичну прогресію задано знаменником Розв'язання: Запишемо формулу сотого елемента прогресії
та знайдемо перший
На основі першого знаходимо 50 член прогресії
Знаходимо суму частини прогресії
та суму перших 100
ЧИТАЙТЕ ТАКОЖ: Квадрати чисел Приклад 4. Знайти число членів арифметичної прогресії, якщо: а3-а1=8, а2+а4=14, Sn=111. Розв'язання: Запишемо рівняння через перший член та крок прогресії та визначимо їх
Отримані значення підставляємо у формулу суми для визначення кількості членів у сумі
Виконуємо спрощення
та розв'язуємо квадратне рівняння
Із знайдених двох значень умові задачі підходить лише число 8. Таким чином, сума перших восьми членів прогресії рівна 111. ЧИТАЙТЕ ТАКОЖ: Формули скороченого множення. Приклади Приклад 5. Розв'язати рівняння 1+3+5+...+х=307. Розв'язання: Дане рівняння є сумою арифметичної прогресії. Випишемо перший її член та знайдемо різницю прогресії
Знайдені величини підставимо в формулу суми прогресії для відшукання кількості доданків
Як і в попередньому завданні, виконуємо спрощення та розв'яжемо квадратне рівняння
Вибираємо більше із двох значень. Маємо, що сума 18 членів прогресії з заданими величинами а1=1,d=2 рівна Sn=307. На цьому знайомство із арифметичними прогресіями завершується. В книжках ви знайдете багато подібних задач та нових, які не були розглянуті. Наведеного матеріалу повинно вистачити Вам з головою, щоб розібратися і роз'вязати задачі самостійно. | ||
|
Схожі матеріали:
| ||
| Всього коментарів: 0 | |
|
ЗАРАЗ ЧИТАЮТЬ
|
|
|
 |  |
 |  |
 |  |
 |  |
 |  |


 Арифметичною прогресією називають послідовність чисел (членів прогресії)
Арифметичною прогресією називають послідовність чисел (членів прогресії)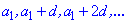
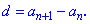
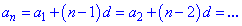
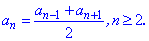
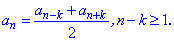
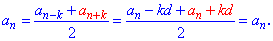
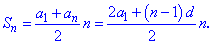
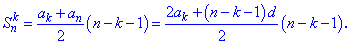
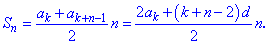
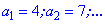
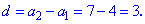
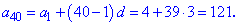
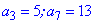 . Знайти перший член прогресії та суму десяти.
. Знайти перший член прогресії та суму десяти.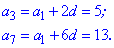
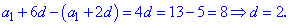
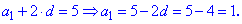
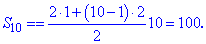
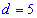 та одним з її членів
та одним з її членів 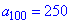 . Знайти перший член прогресії , суму 50 її членів починаючи з 50 та суму 100 перших.
. Знайти перший член прогресії , суму 50 її членів починаючи з 50 та суму 100 перших.