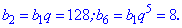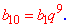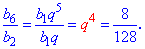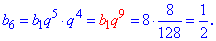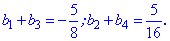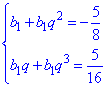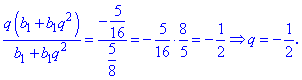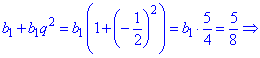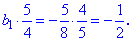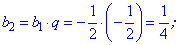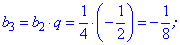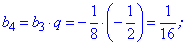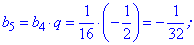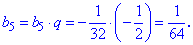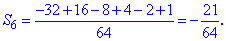|
||||||||
Геометрична прогресія на прикладах
Геометрична прогресія на прикладах
Геометричною прогресією називають таку послідовність чисел Конcтанту, яка характеризує швидкість росту або спадання прогресії називають знаменником геометричної прогресії і позначають
Для повного задання геометричної прогресії окрім знаменника необхідна знати або визначити перший її член. Для додатніх значеннь знаменника 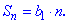 Загальний член геометричної прогресії знаходять за формулою 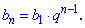 Суму n перших членів геометричної прогресії визначають за формулою 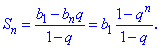 Розглянемо розв'язки класичних задач на геометричну прогресію. Почнемо для розуміння з найпростіших. ------------------------------- Приклад 1. Перший член геометричної прогресії дорівнює 27, а її знаменник рівний 1/3. Знайти шість перших членів геометричної прогресії. Розв'язання: Запишемо умову задачі у вигляді
Для обчислень використовуємо формулу n-го члена геометричногї прогресії
На її основі знаходимо невідомі члени ряду
Як можна переконатися, обчислення членів геометричної прогресії нескладні. Сама прогресія матиме вигляд
----------------------------- Приклад 2. Дано три перших члени геометричної прогресії Розв'язання: Обчислюємо знаменник геомитричної прогресії виходячи з його означення
Отримали знакозмінну геометричну прогресію знаменник якої рівний -2. Сьомий член обчислюємо за формулою
На цьому задача розв'язана. ------------------------------------- Приклад 3. У геометричній прогресіїї Розв'язання: Запишемо задані значення через формули
За правилами потрібно було б знайти знаменник а потім шукати потрібне значення, але для десятого члена маємо
Таку ж формулу можна отримати на основі нехитрих маніпуляцій з вхідними даними. Поділимо шостий член ряду на другий, в резулльтаті отримаємо
Якщо отримане значення помножити на шостий член, то отримаємо десятий
Таким чином для подібних задач за допомогою нескладних перетворень в швидкий спосіб можна отримати правильний розв'язок. ---------------------------------------- Приклад 4. Геометричну прогресію задано рекурентними формулами
Знайти знаменник геометричної прогресії та суму перших шести членів. Розв'язання: Запишемо задані рівняння у вигляді формул
Та виразимо знаменник розділивши друге рівняння на перше
Знайдемо перший член прогресії з першого рівняння
Обчислимо наступні п'ять членів для знаходження суми геометричної прогресії
Оскільки знайти суму в даному випадку не складає великих зусиль, то оминаючи прості викладки зводимо всі доданки під спільний знаменник
В загальному випадку, при знаходженні суми знакозмінних рядів слід виділяти їх додатню частину та від'ємну та знайти окремо їх суми за наведеними вище формулами. Вкінці знайдені значення додати. | ||
|
Схожі матеріали:
| ||
| Всього коментарів: 0 | |
|
ЗАРАЗ ЧИТАЮТЬ
|
|
|
 |  |
 |  |
 |  |
 |  |
 |  |


 Геометрична прогресія не менш важлива в математиці порівняно з арифметичною.
Геометрична прогресія не менш важлива в математиці порівняно з арифметичною.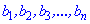 , кожен наступний член якої, отримується домноженням попереднього на стале число.
, кожен наступний член якої, отримується домноженням попереднього на стале число.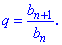
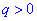 прогресія є монотонною послідовністю, причому якщо
прогресія є монотонною послідовністю, причому якщо 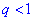 то послідовність чисел є монотонно спадною і при
то послідовність чисел є монотонно спадною і при 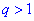 монотонно зростаючою. Випадок, коли знаменник рівний одиниці
монотонно зростаючою. Випадок, коли знаменник рівний одиниці 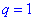 на практиці не розглядається, оскільки маємо послідовність однакових чисел, а їх сумування не важке
на практиці не розглядається, оскільки маємо послідовність однакових чисел, а їх сумування не важке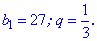
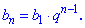
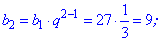
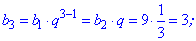
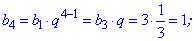
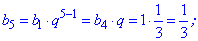
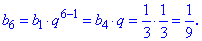
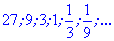
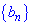 : 6; -12; 24. Знайти знаменник та сьомий її член.
: 6; -12; 24. Знайти знаменник та сьомий її член.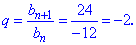
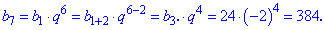
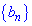 задано двома членами ряду
задано двома членами ряду 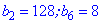 . Знайти десятий член прогресії.
. Знайти десятий член прогресії.