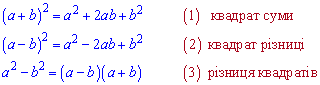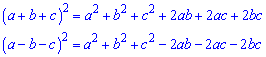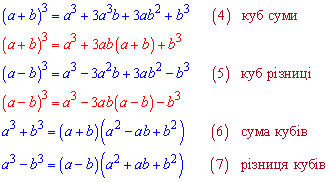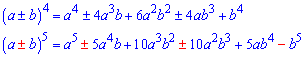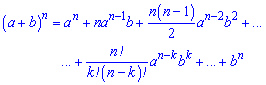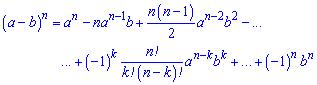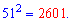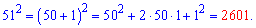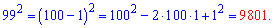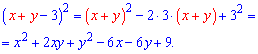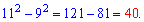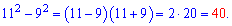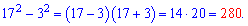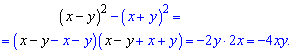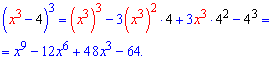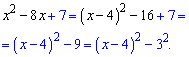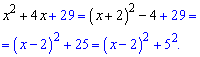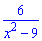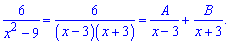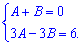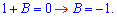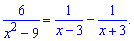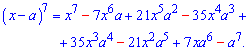Формули скороченого множення. Приклади

Формули скороченого множення застосовують для спрощення обчислень, а також розкладання многочленів на прості множники, швидкого множення многочленів.

Більшість формул скороченого множення можна отримати з біному Ньютона, в цьому Ви скоро переконаєтеся.

Формули для квадратів застосовують в обчисленнях найчастіше.

Їх починають вивчати в шкільній програми починаючи з 7 класу і до кінця навчання формули для квадратів та кубів школярі повинні знати на зубок.

ЧИТАЙТЕ ТАКОЖ: Відсоток від числа

Формули для кубів теж не надто складні і їх потрібно знати при зведенні многочленів до стандартного вигляду, для спрощення піднесення суми чи різниці змінної і числа до кубу.

Формули позначені червоним отримують з попередніх групуванням доданків.

ЧИТАЙТЕ ТАКОЖ: Куб числа

Формули для четвертого степеня та п'ятого степеня в шкільному курсі мало кому пригодяться, однак є завдання при вивченні вищої математики де потрібно обчислювати коефіцієнти при степенях.

Формули для степеня n розписанні через біноміальні коефіціенти з використанням факторіалів наведені нижче

Приклади застосування формул скороченого множення

Приклад 1. Обчислити 51^2.

Розв'язок. Якщо маєте калькулятор то без проблем знаходите

Це я пожартував - з калькулятором мудрі усі, без нього ... (не будемо про сумне).

Не маючи калькулятора та знаючи наведені вище правила квадрат числа знаходимо за правилом

Приклад 2. Знайти  99^2.

Розв'язок. Застосуємо другу формулу

Приклад 3. Піднести до квадрату вираз
 (x+y-3).

Розв'язок. Суму перших двох доданків уявно вважаємо одним доданком і за другою формулою скороченого множення маємо

Приклад 4. Знайти різницю квадратів
 11^2-9^2.

Розв'язок. Оскільки числа невеликі то можна просто підставити значення квадратів

Але мета в нас зовсім інша – навчитися використовувати формули скороченого множення для спрощення обчислень. Для цього прикладу застосуємо третю формулу

Приклад 5. Знайти різницю квадратів
17^2-3^2.

Розв'язок. На цьому прикладі Ви вже захочете вивчити правила, щоб обчислення звести до одного рядка

Як бачите – нічого надзвичайного ми не робили.

Приклад 6. Спростити вираз
(x-y)^2-(x+y)^2.

Розв'язок. Можна розкладати квадрати, а пізніше сумувати подібні доданки. Проте можна прямо застосувати різницю квадратів

Як бачите – нічого надзвичайного ми не робили.

Приклад 7. Піднести до кубу многочлен
 x^3-4.

Розв'язок. Застосуємо 5 формулу скороченого множення

Приклад 8. Записати у вигляді різниці квадратів або сумі
 а) x^2-8x+7
 б) x^2+4x+29

Розв'язок.

а) Перегрупуємо доданки

б) Спрощуємо на основі попередніх міркувань

Приклад 9. Розкласти раціональний дріб

Розв'язок. Застосуємо формулу різниці квадратів

Складемо систему рівнянь для визначення констант

До потроєного першого рівняння додамо друге. Знайдене значення підставляємо в перше рівняння

Остаточно розклад прийме вигляд

Розкласти раціональний дріб часто необхідно перед інтегруванням, щоб понизити степінь знаменника.

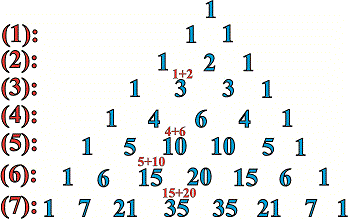
Приклад 10. Використовуючи біном Ньютона розписати
 вираз (x-a)^7.

Розв'язок. Що таке біном Ньютона Ви мабуть вже знаєте. Якщо ні то нижче наведені біноміальні коефіцієнти

Вони утворюються наступним чином: по краю ідуть одиниці, коефіцієнти між ними в нижньому рядку утворюють сумуванням сусідніх верхніх. Якщо ми маємо різницю в якомусь степені, то знаки в розкладі чергуються від плюса до мінуса. Таким чином для сьомого порядку отримаємо такий розклад

Уважно також погляньте як змінюються показники – для першої змінної вони спадають на одиницю в кожному наступному доданку, відповідно для другої – на одиницю зростають. В сумі показники завжди повинні бути рівні степені розкладу (=7).