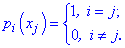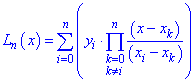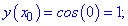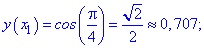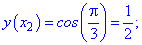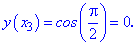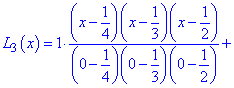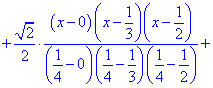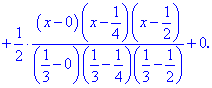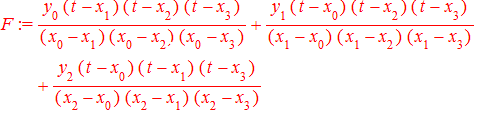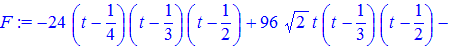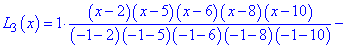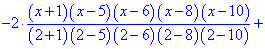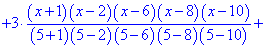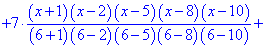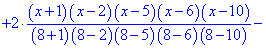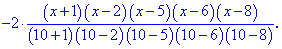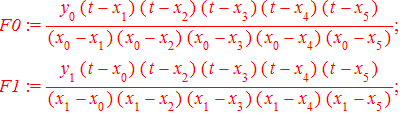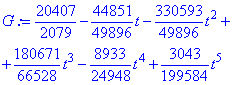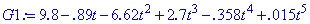|
||||||||
Поліном Лагранжа. Побудова в Maple
Поліном Лагранжа. Побудова в Maple
В загальному - задано таблицю даних вигляду
Потрібно побудувати поліном, який би у вузлах Х[i] приймав значення Y[i]. Цю проблему розв'язав Лагранж, а шуканий поліном має вигляд
де
Функції
Багаточлен вигляду
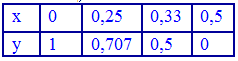
називають інтерполяційним многочленом Лагранжа. Задача1. Для функції у=cos(Pi*x) побудувати інтерполяційний поліном Лагранжа. За вузли інтерполяції взяти точки x[0]=0; x[1]=1/4; x[2]=1/3; x[3]=1/2. Зобразити функцію та вузли на графіку, а також побудувати оригінал. Розв'язання: Обчислюємо значення функції у вузлах
та подаємо у вигляді таблиці
За наведеною вище формулою будуємо інтерполяційний поліном Лагранжа
Спрощувати вручну ми його не будемо. Використаємо для цього математичний пакет Maple, в ньому завдання з вищої математики, фізики, механіки, хімії реалізовують дуже швидко. Задаємо значення функції Далі будуємо інтерполяційний поліном
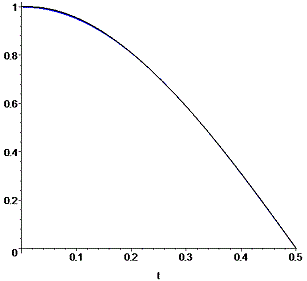
Тут використана змінна t , оскільки змінна x має тип масиву і не може бути використана. Для зручності розкладаємо (series) поліном Лагранжа по степенях Оскільки при змінних в коефіцієнтах містяться корені, то округлюємо (evalf) їх до цілих значень. В результаті отримуємо функцію третього степеня. Далі реалізовуємо побудову графіків цієї функції, оригіналу, та значення функції в точках інтерполяції. > Q1:=plot(G1,t=0..1/2,color=black,thickness=2): Записуємо функцію відображення суперпозиції графіків > display(Q1,Q2);
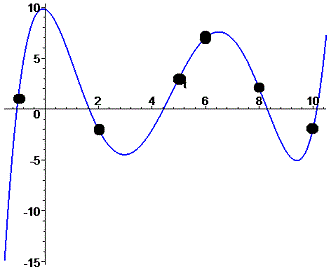
З графіку переконуємося, що різниці між функцією та оригіналом практично немає. Розглянемо інше завдання. Задача 2. Дана таблиця експериментальних даних.
Побудувати інтерполяційний поліном Лагранжа, а також графіки полінома та таблично заданої функції. Розв'язання: Побудуємо інтерполяційний поліном Лагранжа за наведеною вище формулою. Для табличних даних він матиме достатньо громіздкий вигляд, тому випешемо лише його формулу, а решта аналізу виконаємо в Maple.
Далі подібні викладки виконаємо в Maple. Задаємо вузли та значення функції Далі будуємо інтерполяційний поліном Лагранжа. Якщо правою кнопкою мишки вибрати опцію Standard Math то побачимо наступний запис полінома
Після сумування доданків, та розкладу в ряд отримаємо поліном з дробовими коефіцієнтами
які після округлення спрощуємо.
Виконуємо побудову функції
| ||
|
Схожі матеріали:
| ||
| Всього коментарів: 0 | |
|
ЗАРАЗ ЧИТАЮТЬ
|
|
|
 |  |
 |  |
 |  |
 |  |
 |  |


 Інтерполяційний поліном Лагранжа застосовують при наближенні табличних записів даних у вигляді функції, яка є досить добрим наближенням останньої, якщо та мало осцилює і може давати велику похибку, якщо для функцій зі швидкозмінною похідною вибрана мала кількість вузлів інтерполяції.
Інтерполяційний поліном Лагранжа застосовують при наближенні табличних записів даних у вигляді функції, яка є досить добрим наближенням останньої, якщо та мало осцилює і може давати велику похибку, якщо для функцій зі швидкозмінною похідною вибрана мала кількість вузлів інтерполяції.
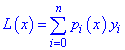
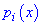 поліноми на одиницю меншого порядку ніж кількість даних, які обчислюють за формулою
поліноми на одиницю меншого порядку ніж кількість даних, які обчислюють за формулою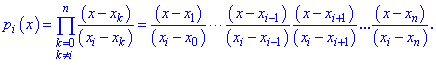
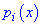 називають лагранжевими коефіцієнтами, вони володіють властивістю
називають лагранжевими коефіцієнтами, вони володіють властивістю