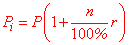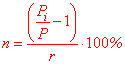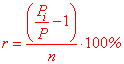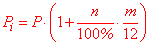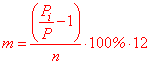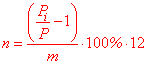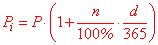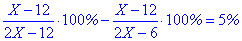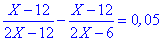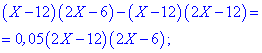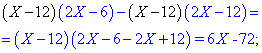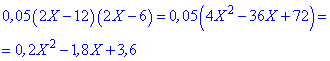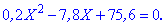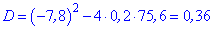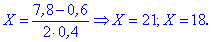Прості відсотки. Задачі та формули

Задачі на прості відсотки зустрічаються в шкільному курсі алгебри, економіці, банківській сфері і т.д. Без розуміння їх змісту та знання формул розв'язати задачі часто буває складно. Нижче на поширених прикладах будуть дані основні задачі та формули для їх розв'язання.

Відсотком (процентом) від числа А називається одна сота частина цього числа. Слово «відсоток» пішло від латинського pro centо, що в перекладі значить «із сотні». Позначення процентів «%» походить від перекручення письмового запису сto.

Наприклад: 10% = 0,1; 10 частина числа А.

У випадку кредитів та депозитів використовують формули для обчислення простих відсотків на період в роках, місяцях і днях. Задачі не вимагають складних обчислень і сподобаються як школярам, так і тим хто впереше знайомиться з відсотками. На практиці відсотки використовують в банківській сфері, хімії, медицині, господарстві.

Інша частина задач стосується знаходження вмісту чогось за відомими відсотками, або навпаки– за вмістом знайти процентні співвідношення.

Обидва типи задач будуть розглянуті нижче.

Простий відсоток на роки

Формула простого відсотку на роки
 P[i]=P*(1+n/100*r)

 де P[i] – збільшення величини P за r років, якщо ставка складає n відсотків. Величиною P можуть виступати депозити, кредити, матеріали.

Задача 1. Вкладник розмістив суму розміром 2400 грн. в банк. Визначте, яку суму отримає вкладник через 3 роки, якщо відсоткова ставка складає 19% в рік.

Розв'язання: Дані з умови підставляємо в формулу простих відсотків
P[3]=2400*(1+19/100*3)=3768 (грн.)

Таким чином за 3 роки вкладник отримає 3768 грн.

Обернена задача на відсотки

Оберненою задачею на відсотки називають таку, в якій за невідомі виступають кількість років або відсоткова ставка.

Задача 2. Вкладник взяв у кредит 3000 грн. і повинен повернути через п'ять років. Знайти відсоткову ставку кредиту, якщо відомо, що потрібно віддати банку 8100 грн.

Розв'язання: Виведемо формулу для цієї задачі.
P[i]=P*(1+n/100*r);
 P[i]/P=1+n/100*r;
n= (P[i]/P-1)/r*100.

Виконуємо обчислення за виведеною формулою
n= (8100/3000-1)/5*100=1,7/5*100=34 (%).
 Отже, відсоткова ставка кредиту складає 34 %.

Якщо в оберненій задачі на відсотки потрібно знайти кількість років, то потрібна формула на основі попередніх викладок матиме вигляд

r= (P[i]/P-1)/n*100

Розрахунок простих відсотків за декілька місяців

Формула простих відсотків в цьому випадку матиме вигляд

P[i]=P*(1+n/100*m/12)

тут позначено m – кількість місяців (month).

Задача 3. Вкладник розмістив суму розміром 1600 грн. в банк один рік, однак йому прийшлося забрати гроші через сім місяців. Відсоткова ставка при достроковому знятті депозиту становить 9 % на рік. Знайти суму, яку отримає вкладник.

Розв'язання:
 Застосовуємо формулу для обчислень

P[3]=1600*(1+9/100*7/12)=1684 (грн.)
 За 7 місяців вкладник отримає 1684 грн.
 З наведеної формули досить просто отримати всі необхідні величини для оберненої задачі.

Кількісць місяців визначають за формулою

m= (P[i]/P-1)/n*100*12

а відсоткову ставку знаходять із залежності

n= (P[i]/P-1)/m*100*12

Розрахунок простих відсотків за період у днях

Даний тип задач застосовують при імітації короткочасних кредитів або депозитів. Формула нарахувань має вигляд

P[i]=P*(1+n/100*d/365)

 тут d – кількість днів.

-----------------------------

Задача 4. Позичальник отримав кредит на суму 20000 грн під 32 % річних. Через 240 днів кредит було повністю погашено. Розрахуйте, яку суму позичальник віддав банку? На скільки різниться ця сума від позиченої?

Розв'язання:
Застосовуємо формулу ростих відсотків для обчислень

P[i]=20000*(1+32/100*240/365)=24208,22 (грн)

Прості відсотки в математиці

Задача 5. У клас закупили 3 енергозберігаючі вікна, які на 20% дорожчі за прості. Скільки витратили грошей, якщо за звичайні вікна потрібно заплатити 1400 грн.

Розв'язання:
Знайдемо ціну енергозберігаючого вікна

P[в]=1400*(1+20/100)=1680 (грн)
 За три вікна заплатили
1680*3=5040 (грн)

-----------------------------

Задача 6. У бочці об'ємом 200 літрів перевозили олію. На станції надібрали 60 літрів. Скільки відсотків від об'єму залишилося?

Розв'язання:
Завдання полягає у знаходженні кількості у процентах олії від загального об'єму бочки.

200-60=140 (л);
 140/200*100%=70 %
 Залишилося 70% об'єму бочки.

-----------------------------

Задача 7. При несвоєчасній сплаті боргів нараховують 2% пені за кожний день просрочення. Яку суму потрібно заплатити через 12 днів після строку погашення 500 грн. боргу?

Розв'язання:
 За формулою простих процентів знаходимо
P[i]=500*(1+2/100*12)=620 (грн)
Потрібно заплатити 620 гривень.

-----------------------------

Розглянемо задачі із підручника для 9 класу авторів А. Г. Мерзляк, В. Б. Полонський, М. С. Якір «Аглгебра».(номер в дужках)

Задача 8. (542) До сплаву масою 600 г, що містить 12 % срібла, додали 60 г срібла. Яким став відсотковий вміст срібла в новому сплаві?

Розв'язання:
 Визначаємо скільки грам срібла в першому сплаві
P[i]=600*12/100=72 (г)
До знайденого значення додаємо 60 грам срібла
P1=72+60=132 (г)

При визначенні відсоткового вмісту срібла не слід забувати, що вага нового сплаву зросла на масу срібла, яку додали.

Якщо б Ви обчислювали наступним чином
132/600*100%=22%
 то отримали б неправильний результат.

ЗАПАМ'ЯТАЙТЕ: в подібних задачах спочатку знаходять міру (вагу, об'єм, довжину) нового об'єкту, а потім знаходять відсотковий вміст.

В заданій задачі новий сплав отримає масу
P2=600+60=660 (г)

а процентний вміст срібла
P1/P2*100%=132/660*100%=20 %
 становитиме 20%.

-----------------------------

Задача 9. (543) У саду росли яблуні й вишні, причому яблуні становили 42 % всіх дерев. Вишень було на 48 дерев більше, ніж яблунь. Скільки дерев росло в саду?

Розв'язання:
 До правильної відповіді можна йти декількома способами. Розглянемо наступний із них.
 Нехай яблуні становлять 42% всіх дерев, тоді вишні
100-42=58%.

Вишень на 48 більше ніж яблук.
 Різниця між ними в процентах становить
58-42=16%
 а в кількості – 48 дерев.

Завдання полягає у знаходженні кількості дерев, тому складаємо відношення

16% – 48 дерев
 100 % –Х дерев

Звідси знаходимо кількість дерев у саду
Х=100*48/16=300 (дерев).

-----------------------------

Задача 10. (544) За два дні було прокладено кабель. За перший день проклали 56 % кабелю, а за другий — на 132 м менше, ніж за перший. Скільки всього метрів кабелю було прокладено за два дні?

Розв'язання:
 Завдання подібне до попередньої задачі. За другий день проклали
100-56=44%
 кабелю, різниця між першим і другим днем становить
56-44=12%
 і складає 132 метри.

На основі цього складаємо відношення
12% – 132 м
100 % –Х м

Звідси знаходимо довжину
Х=100*132/12=1100 (м)

За два дні проклали 1100 м кабелю.

-----------------------------

Задача 11. (545) За перший день хлопчик прочитав 25 % усієї книжки, за другий — 72 % від кількості сторінок, що залишилася, а за третій — решту 84 сторінки. Скільки сторінок у книжці?

Розв'язання:
72 % відсотки від залишку книжки становить
72*(100-25)/100= 54%

На третій день залишалося прочитати
100-25-54=21%
 або 84 сторінки.

Складаємо співвідношення
21% – 84 ст
 100 % –Х ст
 із якого знаходимо
Х=100*84/21=400 (ст),
 що книга містить 400 сторінок.

Складні задачі на прості відсотки

В дану категорію входять задачі, які викликають чимало труднощів у школярів. Проте, якщо достатньо добре розібратися в їх розв'язанні, то всі складнощі відходять на другий план.

Задача 12. (547) Морська вода містить 5 % солі. Скільки прісної води треба додати до 40 кг морської води, щоб концентрація солі становила 2 %?

Розв'язання:
 Знаходимо вагу солі у 40 кг морської води
40*5/100=2 (кг).

Знаходимо вагу води, яка б містила 2% солі (2 кг)
2% – 2 кг
 100 % –Х кг
 або
Х=100*2/2=100 кг.

Зараз у нас є 40 кг води, тому потрібно додати
100-40=60 кг
 прісної води.

-----------------------------

Задача 13. (554) Змішали 30-відсотковий розчин соляної кислоти з 10-відсотковим розчином і отримали 800 г 15-відсоткового розчину. Скільки грамів кожного розчину взяли для цього?

Розв'язання:
 В таких задачах потрібно скласти два рівняння, розв'язування яких і приведе до відшукання потрібних величин.

Позначимо A – вага першого розчину, B – відповідно другого.

Тоді з умови задачі складаємо два рівняння:
 перше стосується процентних співвідношень (*100)
30*A+10*B=800*15
 друге – ваги суміші
A+B=800.

З другого виражаємо одну з невідомих та підставляємо у перше рівняння
A=800-B;
 30*(800-B)+10*B=800*15
 та розв'язуємо його
24000-30*B+10*B=12000;
 20*B=24000-12000=12000;
 B=12000/20=600 (г)

Масу першого розчину знаходимо з залежності
A=800-B=800-600=200 (г).

Отже, потрібно 600 г 30% розчину та 200 г 10 % розчину соляної кислоти.

-----------------------------

Задача 14. (560) До сплаву міді і цинку, який містив міді на 12 кг більше, ніж цинку, додали 6 кг міді. Унаслідок цього відсотковий вміст цинку в сплаві знизився на 5 %. Скільки цинку і скільки міді містив сплав спочатку?

Розв'язання:
 Позначимо вагу міді через X, тоді вага цинку – X-12.
 Відсотковий вміст цинку при цьому становить
(X-12)/(X+X-12)*100%=(X-12)/(2*X -12)*100%.

До сплаву додали 6 кг міді. Вага міді тепер становить X+6,
 а сплаву
X+6+X-12=2*X-6.

Відсотковий вміст цинку в новому сплаві
(X-12)/(2*X-6)*100%

Різниця між попереднім сплавом та новим становить 5%. Це запишемо у вигляді рівняння

Ділимо даний запис на 100 %

 та зводимо до квадратного рівняння (позбуваємося знаменників)

Спрощуємо ліву частину рівняння

 
 та праву

Після перенесення доданків в праву сторону, отримаємо квадратне рівняння

Обчислюємо дискримінант

 та корені рівняння

Отже маємо не один, а пару розв'язків. При 21 кг міді цинку отримаємо

X-12=21-12=9 (кг) ,
 а при 18 кг міді
X-12=18-12=6 (кг).

Отже можливі два сплави – 9 кг цинку і 21 міді, 18 кг цинку і 6 міді. Можете переконатися, що при підстановці в відсоткове рівняння перший сплав міститите 30 % цинку, а другий – 25% цинку.